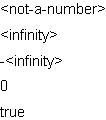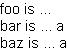| Summary: | - Primitive types are built directly into
the core of the Curl® language.
- There are primitive types for integers,
floating-point numbers, Boolean values,
and characters.
- There are also primitive types for
quantities, such as distance and time.
|
The Curl® language includes support for a number of basic data
types that are built directly into the core of the language.
These basic data types are the primitive types. It
also includes a number of built-in data types that are not
primitive types. These data types are implemented by classes and,
as such, are called class types. Class types are
described in another section of this chapter. Because support for
primitive types is built directly into the core of the language,
working with primitive types is efficient and fast. The Curl
language includes the following kinds of primitive types:
| Summary: | - Integers are whole numbers, with no decimal part.
- Data types: int, int8,
int16, int32,
int64, uint, uint8,
uint16, uint32, uint64,
byte.
- The default value is 0.
- If you exceed the range of values, the value wraps.
|
Use an integer variable to store a whole number (with no decimal
part in the number). For example, 2 is an integer,
whereas 2.5 is not. The Curl language offers a number of
operators for working with integers. To declare an integer
variable, use any of the following data types:
| Data Type | Description | Default Value | Size (Bits) | Legal Range |
|---|
| int | 32-bit signed integer | 0 | 32 | Between -2,147,483,648 and 2,147,483,647 |
| int8 | 8-bit signed integer | 0 | 8 | Between -128 and 127 |
| int16 | 16-bit signed integer | 0 | 16 | Between -32,768 and 32,767 |
| int32 | 32-bit signed integer | 0 | 32 | Between -2,147,483,648 and 2,147,483,647 |
| int64 | 64-bit signed integer | 0 | 64 | Between -9,223,372,036,854,775,808 and 9,223,372,036,854,775,807 |
| uint | 32-bit unsigned integer | 0 | 32 | Between 0 and 4,294,967,295 |
| uint8 | 8-bit unsigned integer | 0 | 8 | Between 0 and 255 |
| uint16 | 16-bit unsigned integer | 0 | 16 | Between 0 and 65,535 |
| uint32 | 32-bit unsigned integer | 0 | 32 | Between 0 and 4,294,967,295 |
| uint64 | 64-bit unsigned integer | 0 | 64 | Between 0 and 18,446,744,073,709,551,615 |
| byte | 8-bit unsigned integer | 0 | 8 | Between 0 and 255 |
The
int32 and
int data types are equivalent. In
fact,
int32 is an alias for
int. Similarly,
uint32 is an alias for
uint, and
byte is an alias for
uint8. See
Integer Literals for information on
integers as literal values.
The following example declares and initializes a number of integer
variables:
| Example:
Declaring and Initializing Integer Variables |
 |
|| Declare and initialize integer variables
{let a:int} || "a" is an int, initialized to 0 (default)
{let b:int=-5} || "b" is an int, initialized to -5
{let c:int=5} || "c" is an int, initialized to 5
{let d:int8=5} || "d" is an int8, initialized to 5
{let e:int8=256 asa int8} || "e" is an int8, initialized to 256
{let f:int16=5} || "f" is an int16, initialized to 5
{let g:int32=5} || "g" is an int32, initialized to 5
{let h:int64=5} || "h" is an int64, initialized to 5
{let i:int=(2.7 asa int)} || "i" is an int, initialized to 2.7
|| Display the integer variables' values
a is ... {value a}{br}
b is ... {value b}{br}
c is ... {value c}{br}
d is ... {value d}{br}
e is ... {value e}{br}
f is ... {value f}{br}
g is ... {value g}{br}
h is ... {value h}{br}
i is ... {value i}
| |
In the example above, notice the following things:
- The variable a is automatically initialized
to the default value (0).
- The variable b is initialized to a negative
value (-5).
- The variable e is initialized to a value
outside of its range, producing an unexpected result.
When declaring an integer variable, be sure to choose a
data type big enough to store its expected values.
- The variable i is initialized to a fractional
number; as a result, the part to the right of the decimal
point is truncated. Similarly, if you assign the result of an
operation that returns a fractional number to an integer, the
part of the result to the right of the decimal point will be
truncated.
Internally, an integer is represented using a scheme that is known
as two's complement form. The details of two's
complement form can be difficult to grasp and are not required to
understand how to work with integers. What is important is to
understand the implications of using two's complement integers.
Basically, you can think of an integer as a value within a
particular range. For example, an int8 is a value between
-128 and 127 inclusive. If you exceed the range of values for one
of the integer data types, the Curl® Runtime
Environment (RTE) does not
generate an error. Instead, the value wraps around to the other
extent of the range. For example, if the value 127 is stored in
an int8 variable and you add one to the variable, the
value of the variable wraps around to -128. Similarly, if the
value -128 is stored in an int8 variable and you subtract
one from the variable, the value of the variable wraps around to
127.
This explains situations in which you might add two large numbers
and get a smaller number as the result. If the sum of the values
is outside the legal range for the data type, the value of the sum
wraps around. The following example shows the sum of two int32 values that is outside the legal range for int32.
| Example:
Illustration of Two's Complement Operation |
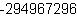 |
{value
|| Declare an "int" variable called "a" and initialize
|| it with the value 2000000000 (within legal range).
let a:int32 = 2000000000
|| Declare an "int" variable called "b" and initialize
|| it with the value 2000000000 (within legal range).
let b:int32 = 2000000000
|| Declare an "int" variable called "c" and initialize
|| it with the sum of "a" and "b" (outside legal range).
let c:int32 = a + b
|| Display the value of "c"
c
}
| |
Generally, you use the int data type when declaring
integer variables. This data type should adequately serve
most purposes. You should also consider that the int
data type, because it typically uses the native word size of a
processor, produces faster code than the other integer data
types. If speed is your main concern, consider using the int data type rather than another integer type.
If space and runtime resources are your main concern, you
might want to use one of the other data types. If you know
the range within which an integer will lie, you can use
int8, uint8, int16, uint16,
int32, uint32, uint64, or int64
to optimize the use of memory by the source code.
There are two constants that might be of interest when
working with
int values:
max-int and
min-int.
max-int is a constant containing
the maximum value that an
int can hold.
min-int is a constant containing the minimum value
that an
int can hold.
| Summary: | - Floating-point numbers have an optional decimal part.
- Data types: float, double.
- double is the default data type for a
floating-point number. To specify a floating-point number
with the float data type, append f
to the number.
- The default value is 0.0.
- A floating-point value represents a specific number, but
the arithmetic operators return the floating-point number
closest in value to the infinitely precise result, due to
the limited precision of floating-point numbers.
- infinity and nan (not a number) are
floating-point constants.
|
Use a floating-point variable to store a number with an optional
decimal part. For example, both 2.0 and 2.5 are
floating-point numbers. To declare a floating-point variable, use
either of the following data types:
| Data Type | Description | Default Value | Size (Bits) | Legal Range |
|---|
| float | IEEE 754 single-precision floating-point
number | 0.0f | 32 | -3.402823466E+38 to
-1.175494351E-38, 0.0, or 1.175494351E-38 to 3.402823466E+38 |
| double | IEEE 754 double-precision floating-point
number | 0.0 | 64 | -1.7976931348623157E+308 to
-2.2250738585072014E-308, 0.0, or 2.2250738585072014E-308 to
1.7976931348623157E+308 |
double is the default data type for a floating-point
number. To specify a floating-point number with the
float data type, append
f to the number.
See
Floating-point
Literals for information on floating-point numbers as literal
values.
The following example shows how to declare and initialize a number
of floating-point variables:
| Example:
Declaring and Initializing Floating-point Variables |
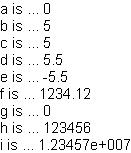 |
|| Declare and initialize floating-point variables
{let a:float} || "a" is a float, initialized to 0.0f (default)
{let b:float=5} || "b" is a float, initialized to 5
{let c:float=5.0f} || "c" is a float, initialized to 5.0f
{let d:float=5.5f} || "d" is a float, initialized to 5.5f
{let e:float=-5.5f} || "e" is a float, initialized to -5.5f
{let f:float=1234.1234f} || "f" is a float, initialized to 1234.1234f
{let g:double} || "g" is a double, initialized to 0.0 (default)
{let h:double=123456.123456} || "h" is a double, initialized to 123456.123456
{let i:double=12345678.12345678} || "i" is a double, initialized to 12345678.12345678
|| Display the floating-point variables' values
a is ... {value a}{br}
b is ... {value b}{br}
c is ... {value c}{br}
d is ... {value d}{br}
e is ... {value e}{br}
f is ... {value f}{br}
g is ... {value g}{br}
h is ... {value h}{br}
i is ... {value i}
| |
In the example above, notice the following things:
- The a and g variables are initialized to
the default value (0).
- When displayed, the redundant decimal places are truncated
for the variable c.
- float constants, as opposed to doubles,
need an f at the end. Usually, you should just use
double unless constraining memory use is particularly
important.
- The variable e is initialized to a negative value
(-5.5f).
- The displayed values of f, h, and i are different from the initialized values. When displaying
floating-point numbers, the runtime uses the default
settings of the format macro. These default settings
display up to six places to the left of the decimal point and
up to two places to the right of the decimal point. If the
number being displayed has more than six places to the left of
the decimal point, scientific notation is used with six digits
of precision.
When a variable is initialized from a literal (for example,
1234.12), the floating-point value mathematically
closest to the represented decimal value is the one stored in
memory. All operations involving this variable use the value in
memory; it is only the display of the number that may be
different. You can use the format macro to change the
way the number is displayed.
Floating-point numbers are stored internally using a scheme
derived from the scientific notation for a decimal number. The
number 2.5 can be represented in this notation as 25e-1, or 2.5e0, or 0.25e+1, and so on. A
floating-point number is normalized when the internal
representation has a mantissa with one non-zero digit before (to
the left of) the decimal point.
A floating-point number consists of a sign, a mantissa, and an
exponent. In the number 0.25e+1, the mantissa is 0.25 and the exponent is +1. The number 0.25e+1
is, like most of the numbers in everyday use, base 10 (decimal).
However, the internal representation of floating-point numbers is
base 2 (binary). Many base 10 floating-point numbers cannot be
represented exactly in base 2. For example, some fractions that
have a terminating decimal representation have an infinitely
repeating binary representation. Consider the decimal number
0.1. When represented in base 2, the number is an
infinite repeating sequence approximated by the number 0.0001100110011001.
When you work with floating-point numbers, be aware that a
floating-point value, while it does represent a specific number,
may be arbitrarily different from the value that one might naively
expect, due to the finite precision and base 2 internal
representation of floating-point numbers. (The process of
determining how well a floating-point program models a
mathematical system is called error analysis and is beyond the
scope of this document.) The fact that the floating-point result
may differ from the mathematical result is a common source of bugs
in code. In most cases, though, if you use double precision
consistently and display only as many significant digits as
necessary, you will obtain useful results.
The following example shows how an arithmetic operator returns
the floating-point number closest in value to the result, rather
than the exact value, due to the limited precision of
floating-point numbers.
| Example:
Floating-point Numbers as Approximations |
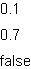 |
|| Declare and initialize a couple of floating-point
|| numbers.
{let f1:float = 0.1f}
{let f2:float = 0.6f}
|| Remember that internally "f1" is represented by an
|| approximation of 0.1. However, the display of "f1"
|| shows the approximation rounded up to 0.1
{value f1}
|| Because the numbers are internally represented by
|| approximations of the real numbers, when you add the
|| numbers you will not get the result that you expect.
|| However, because the difference is so small, the
|| display of the result will be rounded to the expected
|| value.
{value f1 + f2}
|| However, if you compare the actual result to the expected
|| result, they are not equal. The equality operator (==)
|| returns "true" if the values are equal and "false"
|| otherwise. Remember that the internal representation is not
|| the same as the rounded display of the number.
{value f1 + f2 == 0.7}
| |
The only difference between the two types of floating-point
variables (float and double) is the number of bits
used to represent the number. The actual internal representation
of the value is platform-dependent, with different platforms
having different legal ranges for the mantissa and exponent.
Therefore, in theory, the legal range for floating-point values is
platform-dependent. However, the platforms that the runtime
supports in this release conform to the IEEE 754 standard.
Another common source of bugs in code is working with
floating-point numbers whose mantissas or exponents extend beyond
the legal range of values.
Operations involving floating-point numbers do not generate
errors. If a floating-point number is outside the range of
numbers that can be represented on the computer, a special bit
sequence indicates that the number is infinity or negative
infinity. To indicate such numbers, the runtime uses the
printed representations
<infinity> and
-<infinity>.
In a similar manner, the result of an expression that performs an
operation with no defined result is
<not-a-number>. These
special values correspond to the
infinity and
nan global constants.
| Example:
Operations That Result in <infinity> and
<not-a-number> |
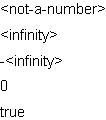 |
|| Divide 0 by 0.
{value 0.0 / 0.0}
|| Divide 1 by 0.
{value 1.0 / 0.0}
|| Divide -1 by 0.
{value -1.0 / 0.0}
|| Divide 0 by 1.
{value 0.0 / 1.0}
|| See if 1 divided by 0 is infinity.
{value (1.0 / 0.0) == infinity}
| |
| Summary: | - Boolean variables store one of two possible values:
true or false.
- The Curl language uses only one bit to internally
represent a Boolean value.
- The Curl language does not support the use of the
numeric values 0 and 1 for
Boolean values.
- Data type: bool.
- The default value is false.
|
Use a Boolean variable to store one of two possible values:
true or
false. The Curl language optimizes the
handling of Boolean values by using only one bit to internally
represent a Boolean value.
To declare a Boolean variable, use the following data type:
| Data Type | Description | Default Value | Size (Bits) | Legal Range |
|---|
| bool | Boolean value | false | 1 | true or false |
Note: In the Curl language, Boolean values are not
interchangeable with numeric values such as 0
and 1.
| Example:
Declaring and Initializing Boolean Variables |
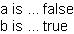 |
|| Declare and initialize Boolean variables
{let a:bool} || "a" is a bool, initialized to false (default)
{let b:bool = true} || "b" is a bool, initialized to true
|| Display the Boolean variables
a is ... {value a}{br}
b is ... {value b}
| |
In the example above, notice the following point:
- The variable a is initialized to the default
value false.
| Summary: | - Characters in the Curl language adhere to the Unicode
Standard.
- Data type: char.
- The default value is \u0000 (Unicode value 0000).
|
Use a character variable to store a single character. Characters
in the Curl®language adhere to the Unicode Standard. As such,
each character has an associated Unicode value, which must be in one of the following ranges:
- 0x0000 - 0xD7FF
- 0xE000 - 0x10FFFF
Values outside of these ranges are not legal values for char.
To specify a character, you can use the
keyboard to enter the character or you
can specify the Unicode value for that character. To declare a
character variable, use the following data type.
| Data Type | Description | Default Value | Size (Bits) | Legal Range |
|---|
| char | Single character | \u0000 (the nul character) | 32 | Between \u0000 and \uD7FF or
\uE000 and \U0010FFFF. |
Note: Many Unicode character expressions may not have a displayable
representation in the font currently in effect on your machine.
If you assign such a value to a variable of type char and
try to display it, your display device (computer or printer) will
use its standard representation for an undisplayable character,
such as a hollow square.
| Example:
Declaring and Initializing Character Variables |
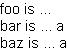 |
|| Declare and initialize character variables
{let foo:char} || "foo" is a char, initialized to \u0000
|| (the default)
{let bar:char='a'} || "bar" is a char, initialized to 'a'
{let baz:char='\u0061'} || "baz" is a char, initialized to \u0061
|| Display the character variables
foo is ... {value foo}{br}
bar is ... {value bar}{br}
baz is ... {value baz}
| |
In the example above, notice the following things:
- The variable foo is initialized to the nul
character (\u0000) by default.
- When assigning a character to a variable, specify a
character literal. Use single quotes (') to surround
the character specification. The character specification can
consist of a keyboard character (a) or a code from the
Unicode Standard (\u0061). To specify a code from the
Unicode Standard, place the characters \u before the
four-digit hexadecimal code.
You can use the addition operator (
+) and the subtraction
operator (
-) with characters. The Unicode values of the
characters are used in the addition or subtraction. When
performing operations on Unicode values, be aware of the range of
legal values for
char.
| Example:
Arithmetic Operations on Characters |
 |
|| Declare a character variable called "foo" that is
|| initialized with the value 'a'.
{let foo:char='a'}
|| Add two to the value of "foo".
{set foo = (foo + 2) asa char}
|| Return the value of "foo".
{value foo}
|| Subtract one from the value of "foo".
{set foo = (foo - 1) asa char}
|| Return the value of "foo".
{value foo}
|| Will cause an error
|| {set foo = '\u0000' - 1 asa char}
| |
| Summary: | - A quantity is a value together with its associated unit
of measurement.
- Data types: Acceleration,
Angle, Area,
Distance, EmDistance,
Fraction,
Frequency, Intensity,
Mass, Percent,
PixelDistance,
Resolution, Speed,
Time.
- 32-bit versions of these data types are also provided:
FloatAngle, FloatArea, and so on.
- New quantity types can be created using type-of.
- The default value is 0.
- Quantities are internally represented as either
float or double values.
|
A quantity is a value together with its associated unit
of measurement. For example, an ordinary value might store the
number three (3), while a quantity might store the value
three centimeters (3cm). Because quantities are primitive
data types, the use of quantities is efficient.
The Curl language includes the following primitive quantity data
types:
Quantities are internally represented
as either
float or
double values. For each type
listed above, there is a corresponding
Float... type with a
32-bit representation; for example,
Distance and
FloatDistance both measure the same thing, but with different
precisions. We recommend you use the
Float... variants only
when conserving space is very important. See
Quantity Literals for information on
quantities as literal values.
Since quantities associate the unit of measurement with the value,
it is easy to work with values that have different units of
measurement. For example, you can compare quantities such as four
inches (4in) and ten meters (10m). Internally,
the value of the quantity is stored with the default unit of
measurement for that quantity. In the case of Distance
quantities, both 4in and 10m are stored as their
equivalent values in meters.
| Example:
Working with Values with Different Units |
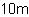 |
|| Declare "d1" a Distance variable and initialize it with
|| the value four inches.
{let d1:Distance = 4in}
|| Declare "d2" a Distance variable and initialize it with
|| the value ten meters.
{let d2:Distance = 10m}
|| Compare d1 and d2 display the greater value.
{if d1 > d2 then
d1
else
d2
}
|| Note that meters, the default unit for Distance quantities,
|| are use to represent Distance quantities internally.
|| By default, a quantity is displayed with the default unit.
| |
Quantities are internally represented as floating-point values.
As such, a quantity is subject to the same constraints regarding
internal representation and precision as a floating-point number.
For example, some numbers that can be exactly represented as a decimal
(base 10) number, such as
0.1, cannot be exactly
represented as a binary (base 2) number. Such constraints and
their implications are outlined in the
Floating-point Numbers section.
You are not restricted to the set of named quantity types above.
The shorthand names are merely a convenience. You can make your
own types if you like, using the
type-of operator.
| Example:
Creating a Custom Quantity Type |
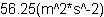 |
|| Define one speed.
{let s1:Speed = 15m / 2s}
|| Another way to write the same value:
{let s2:Speed = 7.5(m/s)}
|| Let's make a funny new quantity type that has no name.
{let speed-squared:{type-of 1(m^2/s^2)} = s1 * s2}
{value speed-squared}
| |
See the
Quantities and
Units chapter for more information about quantities, including a
list of valid unit specifiers and information about operations
involving quantities.
Copyright © 1998-2019 SCSK Corporation.
All rights reserved.
Curl, the Curl logo, Surge, and the Surge logo are trademarks of SCSK Corporation.
that are registered in the United States. Surge
Lab, the Surge Lab logo, and the Surge Lab Visual Layout Editor (VLE)
logo are trademarks of SCSK Corporation.